How To Find The Base Of An Exponential Graph

What Are Exponential Functions?

Before we become into dealing with exponential functions and graphing exponential functions, let's beginning accept a look at the general formula and theory behind exponential functions.

Below is 1 of the most full general forms of an exponential graph:

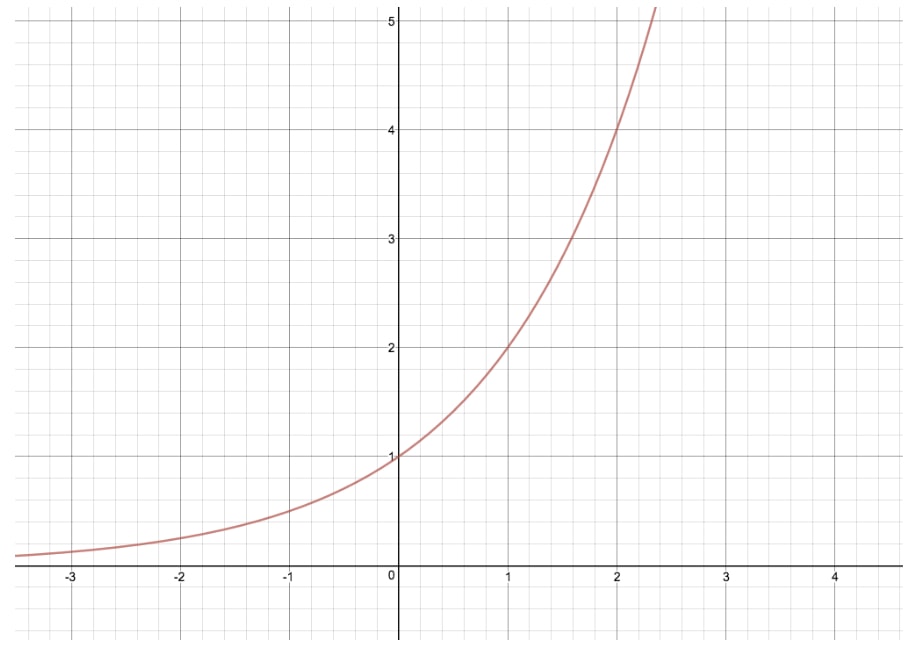
The exponential function equation to this graph is $y=2^10$ , and is the most elementary exponential graph we can make. If you're wondering what $y=1^ten$ would expect like, here'southward its exponential graph:

Now, as to the reason why the graphs of $y=2^x$ and $y=one^x$ are so different, the all-time mode to understand the theory behind exponential functions is to take a expect at some tables.

The table of values of y = 1^x and y = 2^x — The table of values of y = ane^ten and y = two^x

Above you can see 3 tables for three different "base values" – 1, 2 and 3 – all of which are to the power of ten. As y'all can see, for exponential functions with a "base value" of 1, the value of y stays constant at 1, because 1 to the power of anything is just ane. That is why the above graph of $y=1^10$ is merely a directly line. In the instance of $y=2^x$ and $y=3^x$ (not pictured), on the other hand, we see an increasingly steepening curve for our graph. That is because equally x increases, the value of y increases to a bigger and bigger value each time, or what we telephone call "exponentially".

Now that we have an idea of what exponential equations wait similar in a graph, let's give the general formula for exponential functions:

$y=ab^{d(ten-c)}+one thousand$

The above formula is a fiddling more complicated than previous functions you've likely worked with, and then permit's define all of the variables.

y – the value on the y-axis

a – the vertical stretch or compression factor

b – the base value

x – the value on the ten-centrality

c – the horizontal translation factor

d – the horizontal stretch or compression gene

thou – the vertical translation factor

In this lesson, we'll just be going over very bones exponential functions, so you lot don't need to worry near some of the higher up variables. Just, so you accept admission to all of the data you need near exponential functions and how to graph exponential functions, let'due south outline what irresolute each of these variables does to the graph of an exponential equation.

one) Variable "a"

Let's compare the graph of $y=ii^x$ to some other exponential equation where we modify "a", giving us $y=(-iv)ii^10$

Compare the graph of y = 2^x and y = (-4)2^x — Compare the graph of y = 2^x and y = (-4)2^ten

Past making this transformation, nosotros take both "stretched" and "reflected" the original graph of $y=ii^x$ past it'due south y-values. In order to find "a" past looking at the graph, the most important thing to detect is that when x=0 and we don't have a value for "k", the y-intercept of our graph is always going to be equal to "a".

2) Variable "b"

Besides known as the "base value" this is merely the number that has the exponent fastened to information technology. Finding information technology involves algebra, which will be discussed later in this commodity.

Variable "c"

Let'southward compare the graph of $y=2^x$ to some other exponential equation where we modify "c", giving us $y=2^{(ten-2)}$

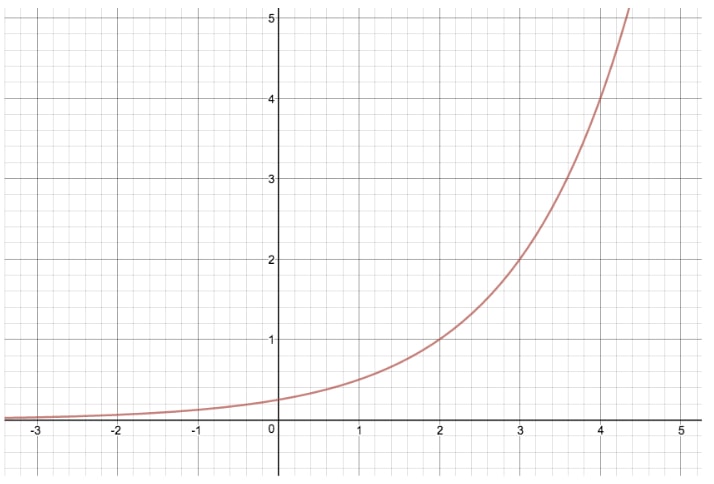
Compare the graph of y = 2^x and y = x^(x-2) — Compare the graph of y = 2^x and y = x^(ten-2)

By making this transformation, we have shifted the entire graph to the correct 2 units. If "c" was equal to -2, nosotros would accept shifted the entire graph to the left two units.

Variable "d"

Let's compare the graph of $y=2^10$ to another exponential equation where we modify "d", giving united states $y=2^{4x}$

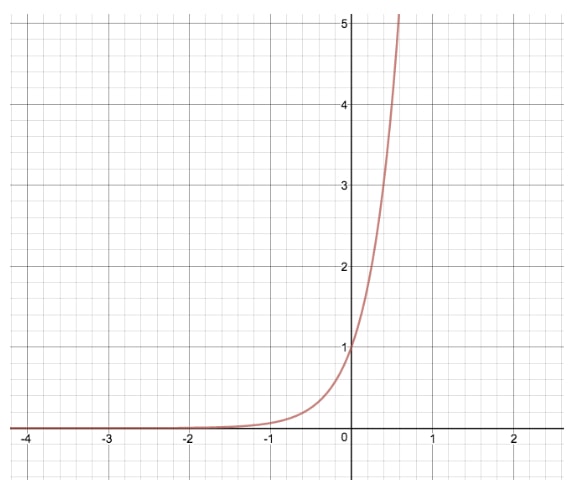
Compare the graph of y = 2^x and y = 2^(4x) — Compare the graph of y = ii^x and y = 2^(4x)

Past making this transformation, we have stretched the original graph of $y=2^x$ by its 10-values, similar to how the variable "a" modifies the function past its y-values. If "d" were negative in this case, the exponential role would undergo a horizontal reflection as opposed to the vertical reflection seen with "a".

Variable "k"

Let's compare the graph of $y=2^x$ to another exponential equation where nosotros modify "k", giving us $y=2^x+ii$

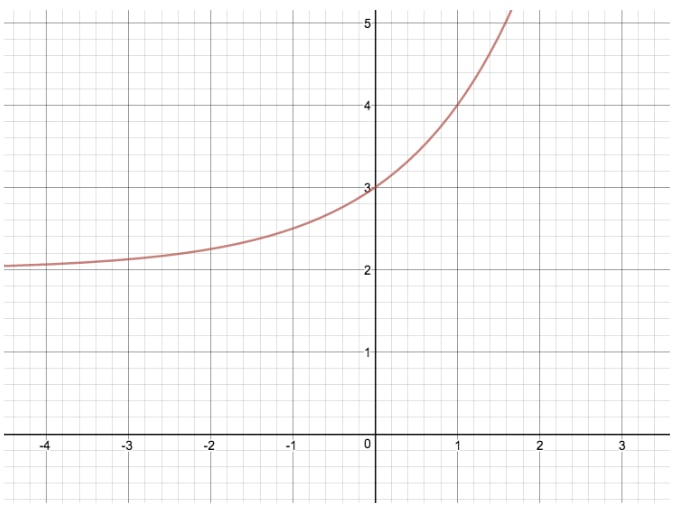
Compare the graph of y = 2^x and y = 2^x + 2 — metric conversion table (length)

By making this transformation, we take translated the original graph of $y=2^x$ up two units. If "k" were negative in this instance, the exponential office would have been translated down 2 units. "k" is a particularly important variable, as information technology is likewise equal to what we call the horizontal asymptote! An asymptote is a value for either x or y that a role approaches, but never actually equals.

Have for example the role $y=2^x$ : for this exponential role, k=0, and therefore the "horizontal asymptote" equals 0. This makes sense, because no matter what value we put in for x, we will never get y to equal 0. For our other function $y=2^x+2$ , k=2, and therefore the horizontal asymptote equals 2. There is no value for x we tin can utilise to make y=2.

And that's all of the variables! Again, several of these are more than complicated than others, and so it will take time to get used to working with them all and becoming comfortable finding them. To become a better await at exponential functions, and to go familiar with the in a higher place general equation, visit this excellent graphing calculator website here. Take your fourth dimension to play around with the variables, and get a better feel for how changing each of the variables effects the nature of the function.

At present, let's go downwardly to business. Given an exponential function graph, how can we notice the exponential equation?

How To Find Exponential Functions

Finding the equation of exponential functions is oftentimes a multi-step process, and every problem is different based upon the information and type of graph we are given. Given the graph of exponential functions, we need to be able to take some information from the graph itself, and then solve for the stuff nosotros are unable to accept directly from the graph. Below is a listing of all of the variables we may have to await for, and how to ordinarily find them:

a – solve for it using algebra, or it will be given

b – solve for information technology using algebra, or it volition be given

c – let 10 = 0 and imagine "c" is not there, the value of y will equal the y-intercept; now count how many units the y value for the y-intercept is from the y-centrality, and this will equal "c"

d – solve for it using algebra

grand – equal to the value of the horizontal asymptote

Of course, these are just the general steps you demand to take in club to observe the exponential office equation. The best way to learn how to do this is to try some practice issues!

Exponential Functions Examples:

At present let'southward effort a couple examples in order to put all of the theory we've covered into practice. With practice, you'll be able to detect exponential functions with ease!

Case 1:

Determine the exponential part in the form $y=ab^x$ of the given graph.

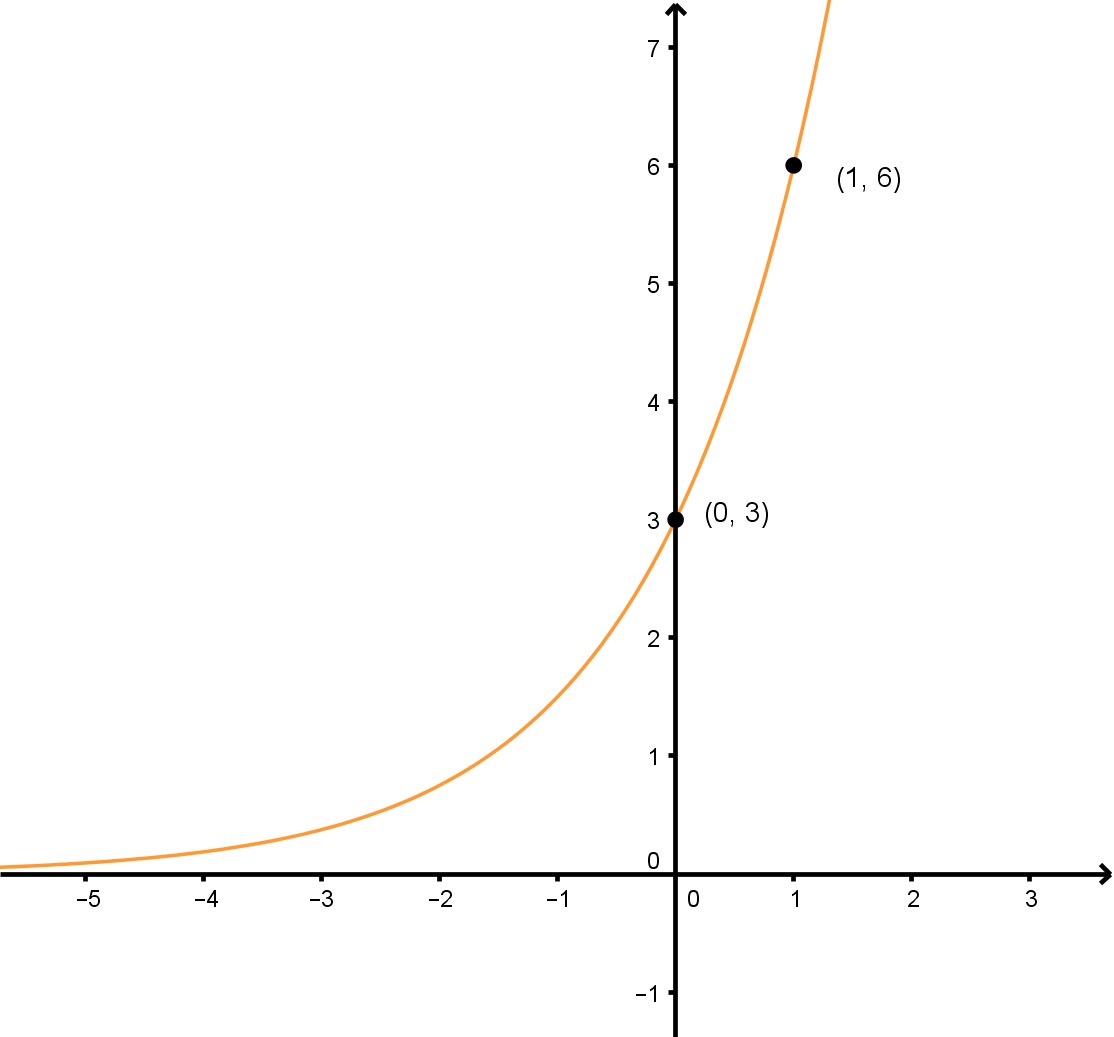
Finding an exponential function given its graph

In order to solve this problem, we're going to need to detect the variables "a" and "b". As well, nosotros're going to take to solve both of these algebraically, equally we tin't decide them from the exponential role graph itself.

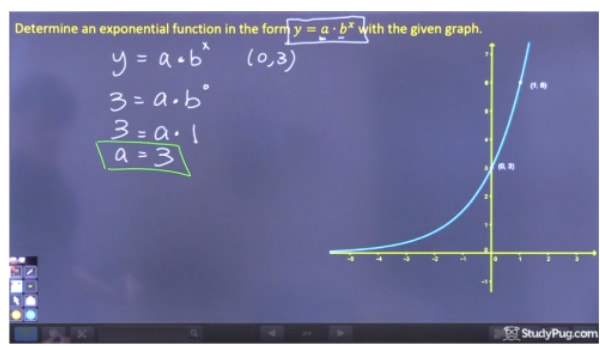
Step ane: Solve for "a"

To solve for "a", nosotros must pick a point on the graph where we can eliminate bx because we don't yet know "b", and therefore we should option the y-intercept (0,iii). Since b0 equals 1, we can discover that a=three. As a shortcut, since we don't' accept a value for g, a is only equal to the y-intercept of this equation.

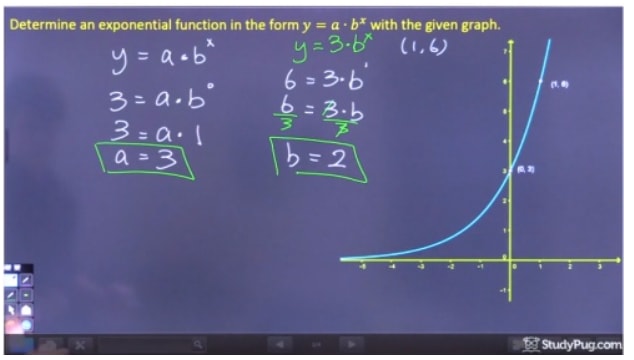
Step 2: Solve for "b"

Now that we have "a", all we have to do is sub in 3 for "a", choice another betoken, and solve for b. Let's choice the point (one,6). With all this information, nosotros tin find that b=2.

Find b of the equation y = a b^x — Notice b of the equation y = a b^x

Step 3: Write the Concluding Equation

Now we that we have found all of the necessary variables, all that'south left is to write out our final equation in the form $y=ab^x$ . Our final reply is $y=(3)ii^10$

Write the final equation of y = a b^x — Write the final equation of y = a b^ten

Example 2:

Determine the exponential function in the form $y=a2^{dx}+k$ of the given graph.

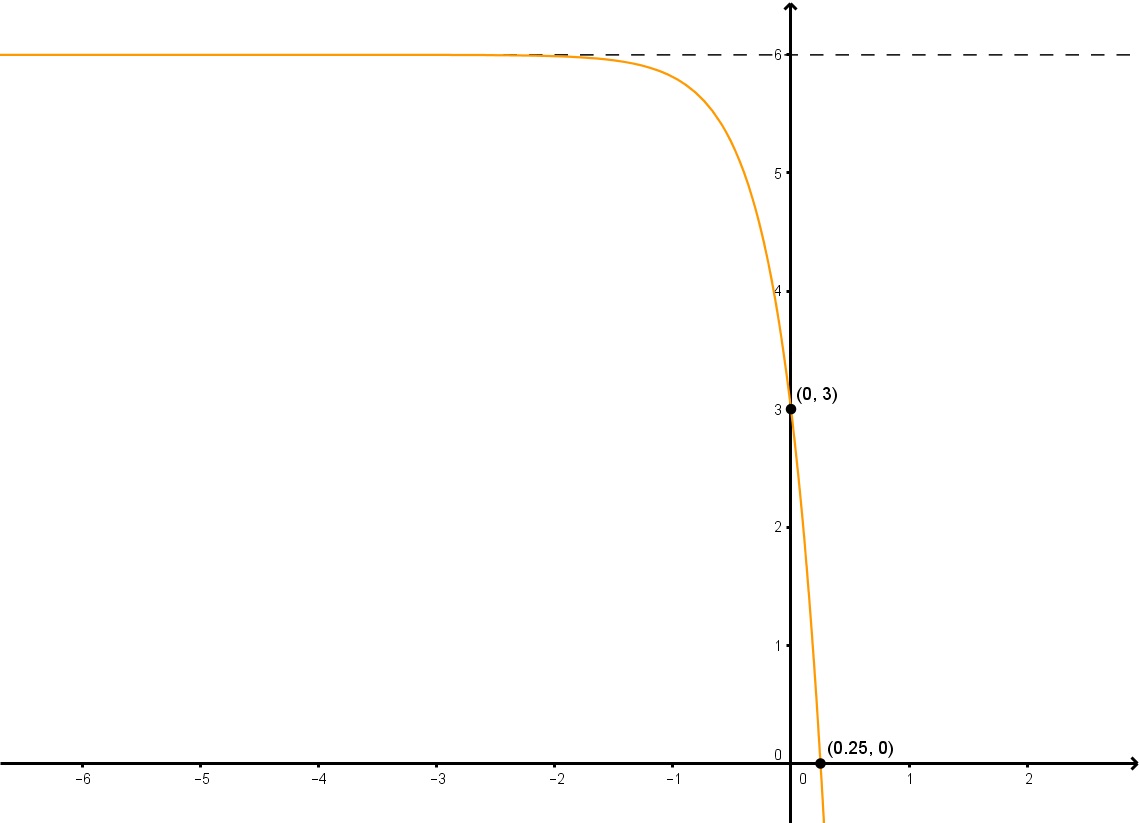
In order to solve this trouble, we're going to demand to find the variables "a", "d" and "k". Recollect, nosotros tin can find "k" from the graph, as information technology is the horizontal asymptote. For "a" and "d", notwithstanding, we're going to have to solve for these algebraically, as nosotros can't determine them from the exponential function graph itself.

Step 1: Notice "k" from the Graph

To find "k", all we need to practise is notice the horizontal asymptote, which is conspicuously y=6. Therefore, thousand=half-dozen.

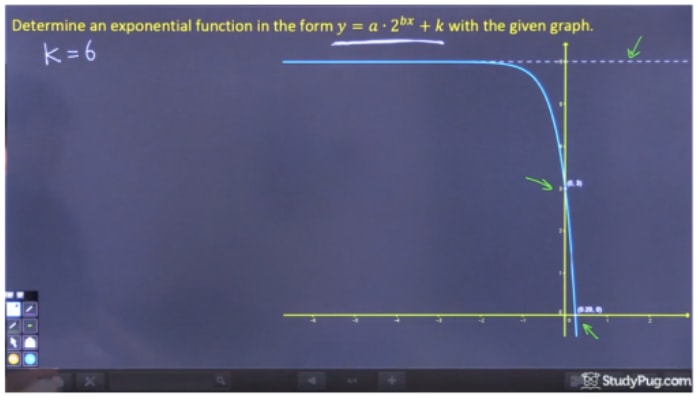
Find k of the equation y = a 2^(bx) + k — Find yard of the equation y = a 2^(bx) + k

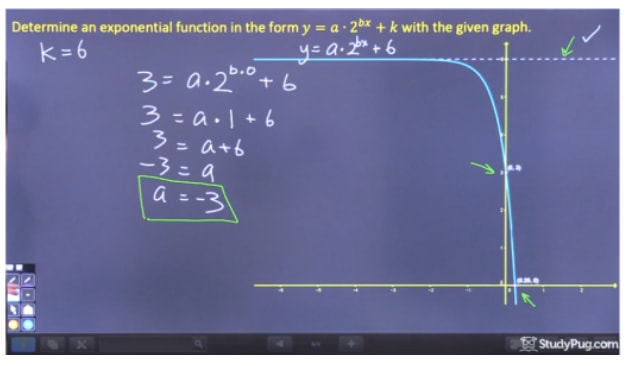
Step ii: Solve for "a"

To solve for "a", just like the last instance, we must pick a bespeak on the graph where nosotros tin can eliminate 2dx because we don't notwithstanding know "d", and therefore we should pick the y-intercept (0,3). Since twenty equals 1, subbing (0, iii) into $y=a2^{dx}+6$ gives us that a=-3.

Find a of the equation y = a 2^(bx) + k — Find a of the equation y = a ii^(bx) + thousand

Step three: Solve for "b"

Now that we have "a" and "k", all nosotros have to do is pick some other point and solve for b. Let's choice the point (0.25, 0). With all this information, we can find that d=4.

Find b of the equation y = a 2^(bx) + k — Find b of the equation y = a ii^(bx) + k

Footstep 4: Write the Terminal Equation

At present we that we have found all of the necessary variables, all that's left is to write out our final equation in the form $y=ab^{dx}+g$ . Our final reply is $y=(-3)2^{4x}+6$

Write the final equation of y = a 2^(bx) + k

And that's information technology for exponential functions! Over again, these functions are a little more than complex than equations for lines or parabolas, so exist certain to exercise lots of exercise issues to get a hang of the new variables and techniques. With more practise, before long exponential equations and the graphs of exponential functions will be no problem at all!