How To Find Dy 2 Dx 2
The second derivative is what y'all get when you differentiate the derivative. Remember that the derivative of y with respect to x is written dy/dx. The second derivative is written d2y/dx2, pronounced "dee ii y by d ten squared".
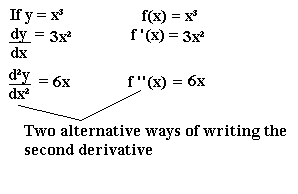
Stationary Points
The 2nd derivative can be used as an easier manner of determining the nature of stationary points (whether they are maximum points, minimum points or points of inflection).
A stationary bespeak on a curve occurs when dy/dx = 0. Once you have established where there is a stationary indicate, the type of stationary point (maximum, minimum or indicate of inflexion) can be adamant using the second derivative.
| If | d2y | is positive, then it is a minimum point |
| dxtwo |
| If | d2y | is negative, then it is a maximum point |
| dx2 |
| If | d2y | = nada, and so information technology could be a maximum, minimum or point of inflexion |
| dx2 |
If d2y/dx2 = 0, you must exam the values of dy/dx either side of the stationary point, as earlier in the stationary points department.
Instance
Find the stationary points on the curve y = 103 - 27x and decide the nature of the points:
At stationary points, dy/dx = 0
dy/dx = 3x2 - 27
If this is equal to aught, 3xtwo - 27 = 0
Hence 10two - 9 = 0 (dividing by 3)
So (x + 3)(10 - iii) = 0
So x = 3 or -3
d2y/dxii = 6x
When x = 3, diiy/dx2 = 18, which is positive.
When 10 = -3, d2y/dxii = -xviii, which is negative.
Hence in that location is a minimum signal at x = 3 and a maximum point at x = -3.
Source: https://revisionmaths.com/advanced-level-maths-revision/pure-maths/calculus/second-derivative
Posted by: krollevessureary.blogspot.com


0 Response to "How To Find Dy 2 Dx 2"
Post a Comment