What Is a Centroid?

The centroid is a geometric property of a shape, somewhat related to the center of mass. It is the point denoted (x̄, ȳ) that is the boilerplate of all points in the shape. For example, in a rectangle the average of all points in the shape is dead center, as shown in Figure 1 below.

Figure 1, the centroid of a rectangle

Figure i. The average position of all points, or centroid, of a rectangle is precisely in the middle of the shape.

The centroid tin can exist used every bit the center of mass if we assume the mass of the shape to be evenly spread throughout. With this definition, the centroid is the point at which y'all could balance the shape on the tip of a pencil. If the centroid is non within the shape, as in Figure 2 below, then it is not possible to residual the shape in such a style.

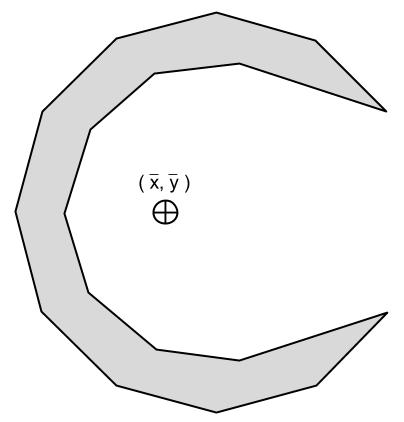
Figure 2, the centroid of a crescent moon

Figure ii. The centroid of a crescent is not inside the bounds of the shape, so in that location is no point on which it tin can be balanced.

Complex shapes can be broken down into simpler component shapes to make calculations easier. For example, nosotros don't know intuitively how to calculate the centroid of the shape shown in Figure 3 below, but we have a formula for its rectangular pieces. The centroid of the overall shape is the weighted average of the centroids of its elective parts. In precise terms, if we separate a shape into northward regions with areas Aone, A2, ..., Anorthward and centroids (x̄ane, ȳane), (x̄ii, ȳ2), ..., (x̄due north, ȳn), the centroid of the original shape would be:

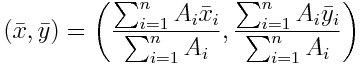
Summation notation for the centroid

Applying these equations to the T shape in Figure 3 below, we can calculate the location of the overall centroid as:

Formula for the centroid of the T shape in Figure 3

Figure 3, finding the centroid of a complex shape.

Effigy 3. Nosotros can discover the centroid of a complex shape by taking the weighted boilerplate of the centroids of its constituent pieces.

Why Is This Useful?

Our goal here is to discover the centroid of any polygon past using a simple algorithm. This is useful because we tin extend it to include shapes with curved edges, as in Figure 4 below. The centroid of a shape with shine curved edges can exist approximated by replacing the curve with a segmented approximation. We did something like already in the crescent of Figure 2 above.

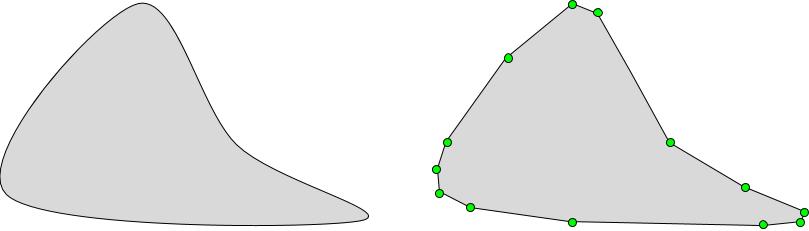
Figure 4, approximating curves with segmentation

Figure four. The curved shape on the left above can be approximated past replacing its curved edges with straight line segments, forming a polygon as shown on the right. Nosotros can then approximate the centroid of the resulting polygon.

The centroid is also useful when you need to become the heart of mass for an object of uniform mass distribution. This comes in handy for all sorts of things, from implementing physics in a computer game to calculating the maximum expected stress on an I-axle.

The only caveat with our algorithm is that the polygon must be non-intersecting. This is often the example, as a self-intersecting polygon doesn't model a physical object in the real world.

What Is a Non-Intersecting Polygon?

In this context, nosotros will define a non-intersecting polygon to exist a polygon in which no ii edges intersect with each other. The shapes that nosotros typically consider such as rectangles, triangles, trapezoids, etc. are all non-intersecting. Nosotros define a self-intersecting polygon to be a shape in which at least 2 edges intersect with each other, such as the hourglass shape in Figure 5 below.

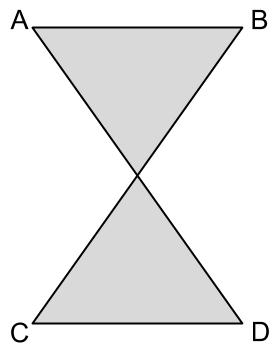
Figure 5, a self-intersecting polygon

Figure 5. The hourglass shape above is self-intersecting, and using it as input to our algorithm will yield incorrect results.

The Algorithm

The polygon that we use equally input to the algorithm we will denote as the ordered set up of vertices P = { vone, vii, ..., vn }.

Getting the Expanse and Centroid of a Triangle

The footing of our algorithm volition rest upon the supposition that we know how to get the area and centroid of a triangle, given the coordinates for its 3 vertices. Given a triangle ABC, we can calculate the components of ii vectors AB and AC, as shown in Figure half-dozen beneath.

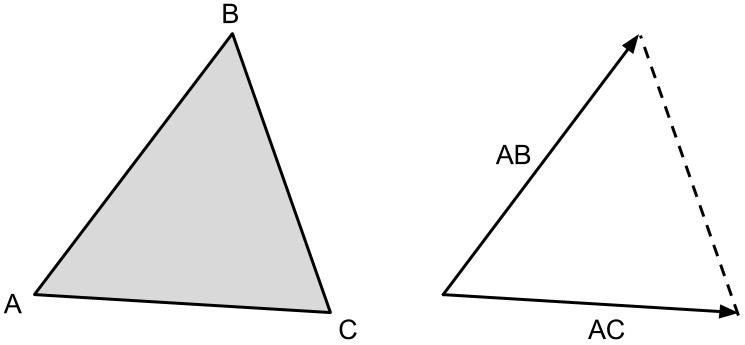
Figure 6, turning a triangle into vectors.

Figure 6. Going from a triangle to a pair of vectors.

Past taking the cross production of the two vectors, Ac × AB, we become a resulting vector that has the magnitude of the surface area of the parallelogram that is spanned past AB and BC. Past cut this area in one-half, nosotros get just the area of the triangle ABC. This is shown in Figure 7 below.

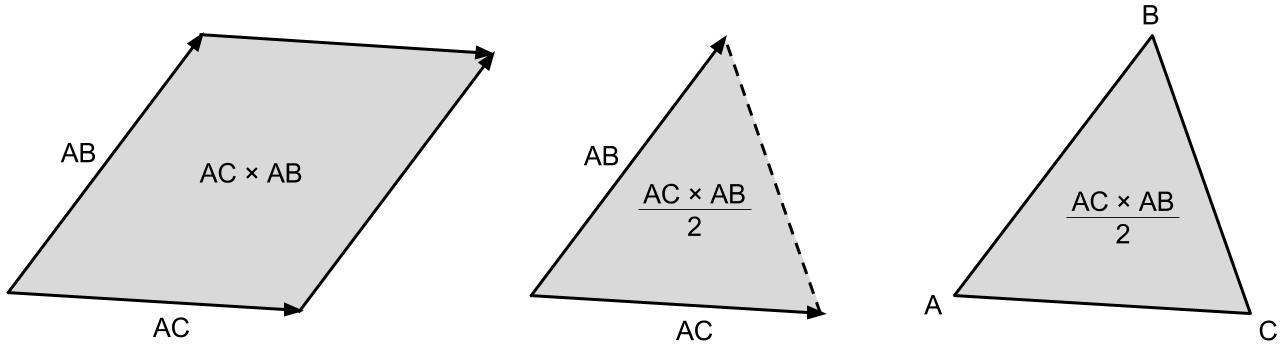
Figure 7, turning vectors into the area of the triangle.

Figure seven. Going from a pair of vectors dorsum to the area of the triangle.

Because of the correct-paw dominion, taking the cantankerous product Air conditioning × AB gives united states of america a positive consequence if the triangle ABC is right-handed (its vertices are clockwise) and gives united states of america a negative result if information technology is left-handed (its vertices are counterclockwise). However, this signed area will plough out to exist necessary for our algorithm. Working out the algebra results in the following closed formula for the signed area of triangle ABC:

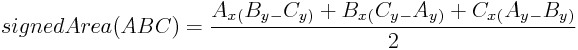
Formula for the signed area of a triangle ABC

Side by side we have to observe the centroid of the triangle. We will apply elementary geometry to find a airtight formula, although it is possible to use an algebraic argument too. If we carve up triangle ABC into n dissever strips with edges parallel to side BC as shown on the left in Figure 8 below, we tin can use the weighted average of their centroids as the overall centroid of the triangle. As northward becomes big, the strips get very sparse, and their centroids approach the midpoint of their two endpoints. For the longest strip, this centroid is the midpoint of points B and C. The centroids for the other strips all follow a straight line from the midpoint of side BC through signal A. Any weighted average of these points must also lie along the directly line they brand.

We can make a similar argument using north strips parallel to side AB or AC to testify that the centroid of the triangle must lie on the line betwixt the midpoint of side AB and point C as well as the line betwixt the B and the midpoint of side AC and point B. The merely way for the centroid to lie on all three of these lines at once is if information technology is located at their intersection.

Figure 8, geometric proof that the centroid of a triangle must be located at the intersection of lines from a vertex to the midpoint of the opposite edge.

Figure viii. On the left nosotros have the triangle ABC split into strips parallel to side BC, with centroids that form a straight line from the midpoint of BC to point A. The right side shows the location of the triangle'south centroid, which is at the intersection of all three such lines.

At present that nosotros know where the centroid of a triangle is geometrically, how do nosotros summate information technology numerically from the coordinates of its vertices? Note that when nosotros accept the boilerplate of three vertices A, B, C, we can outset by taking the boilerplate of any pair of the vertices to get a midpoint M. We can and so average the remaining vertex with K, which must result in a point on the line between M and the remaining vertex. Since nosotros can choose any 2 vertices for M, the boilerplate of A, B, C must exist on the line between A and the midpoint of BC, the line betwixt B and the midpoint of Air-conditioning, and the line betwixt C and the midpoint of AB. Therefore the boilerplate of the vertices A, B, C is precisely the centroid of the triangle ABC, as shown on the correct in Figure 8 above. This gives us the following closed formula:

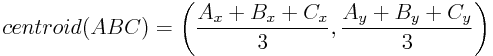
Formula for the centroid of triangle ABC

Splitting the Polygon Into Triangles

Since we accept a mode to summate the area and centroid of a triangle, and nosotros take a way to calculate the centroid of a complex shape given the areas and centroids of its component parts, the next logical step is to split the polygon P into triangles. We practise this by taking any three consecutive vertices A = vi , B = vi+ane , C = 5i+2 in P and forming a triangle ABC. The state of affairs so far is shown in Effigy 9 below.

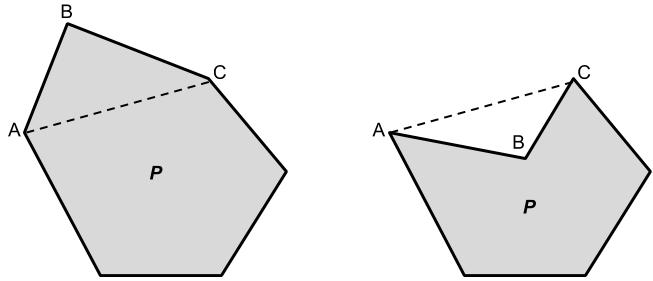
Figure 9, creating a triangle from three consecutive vertices.

Figure nine. The ii possible scenarios when forming a triangle from three sequent vertices. Either the triangle is function of the polygon P as shown on the left, or it is empty space equally shown on the right.

The algorithm keeps a running count Atotal of the full area of P and a running average (x̄total, ȳtotal) of the centroid calculated then far. We add each triangle ABC's area to Atotal and average its centroid into (x̄total, ȳfull). Next we remove the vertex B from P , forming the smaller polygon P' = P – { B }.

If the triangle ABC is part of the polygon P as on the left in Figure ix, so ABC will be right-handed and its area will be positive. Removing B removes ABC's area from ***P'***, and so ABC's area and centroid will count positively toward Atotal and (x̄total, ȳfull) overall. On the other mitt, if the triangle ABC is empty space as on the correct in Figure nine, then ABC will exist left-handed and its surface area will be negative. All the same, removing B adds ABC's area to ***P'***, and then ABC's expanse and centroid will count positively toward the totals due to another triangle in ***P'***. Since ABC counts negatively toward Afull and (x̄total, ȳtotal) and then positively, information technology makes no impact overall. This is what we expect, as in this case ABC is empty space. The event of removing vertex B is shown in Effigy 10 below.

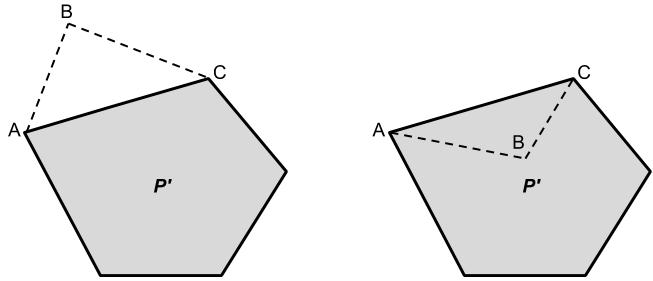
Figure 10, removing vertex B from the polygon.

Figure 10. The result of removing vertex B from the polygon P is shown higher up, both in the case where ABC is part of P (left) and in the case where ABC is empty infinite (right).

We go on in this fashion, setting P equal to ***P'***, and removing a vertex each time until P' has less than 3 vertices and thus tin can't form a triangle. Then Atotal and (x̄total, ȳtotal) are the overall signed expanse and centroid of the original polygon P .

Runtime Analysis

The polygon begins with northward vertices, and with each iteration of the algorithm information technology removes a vertex. Since it terminates when the polygon has less than iii remaining vertices, information technology runs for a maximum of n – 2 = O(n) steps. With each step, nosotros have to calculate the signed area and centroid of a triangle and boilerplate them into the running total for the polygon. These calculations take a constant amount of time, and then overall the algorithm runs in O(north) fourth dimension. This means the amount of steps the algorithm has to take increases linearly with the number of vertices in the polygon.

Notwithstanding, if we wanted to bank check the polygons to make sure that they were non-intersecting before running the algorithm, we would accept to cheque every edge confronting every other edge. This would increase the run time of the algorithm to O(n 2). For polygons with a big number of vertices, checking for cocky-intersection would dramatically increase the number of steps in the algorithm.

Python Implementation

The post-obit is an implementation of the algorithm in Python. Given a list of three or more points, it returns the centroid of the polygon that they form.